7 Key Facts About Debye Relaxation Process

Understanding the Debye Relaxation Process

The Debye relaxation process is a fundamental concept in physics and chemistry that describes the relaxation behavior of dielectric materials. This process is crucial in understanding various phenomena, including the response of materials to external electric fields and the dynamics of molecular motions. Here are 7 key facts about the Debye relaxation process that provide a comprehensive overview of this essential concept.
What is the Debye Relaxation Process?
The Debye relaxation process is a mathematical model developed by Peter Debye in 1913 to describe the relaxation behavior of dielectric materials. It is a classical model that explains the exponential decay of the electric polarization in a material after the removal of an external electric field. The model assumes that the material is composed of non-interacting dipoles that rotate freely in response to the external electric field.
Key Characteristics of the Debye Relaxation Process

The Debye relaxation process has several key characteristics that are essential to understanding its behavior:
- Exponential Decay: The Debye relaxation process is characterized by an exponential decay of the electric polarization with time.
- Single Relaxation Time: The Debye model assumes a single relaxation time, which is a measure of the time it takes for the material to return to its equilibrium state after the removal of the external electric field.
- Temperature Dependence: The relaxation time is temperature-dependent, with higher temperatures resulting in shorter relaxation times.
Equations Describing the Debye Relaxation Process
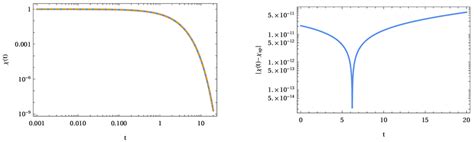
The Debye relaxation process is mathematically described by the following equations:
- Debye Equation: The Debye equation describes the exponential decay of the electric polarization with time:
P(t) = P0 * exp(-t/τ)
where P(t) is the electric polarization at time t, P0 is the initial polarization, and τ is the relaxation time.
- Kohlrausch-Williams-Watts (KWW) Equation: The KWW equation is a modified version of the Debye equation that takes into account the non-exponential decay behavior observed in many materials:
P(t) = P0 * exp(-(t/τ)^β)
where β is a parameter that describes the degree of non-exponentiality.
Applications of the Debye Relaxation Process
The Debye relaxation process has numerous applications in various fields, including:
- Dielectric Spectroscopy: The Debye relaxation process is used to analyze the dielectric properties of materials and understand their behavior under different conditions.
- Materials Science: The Debye model is used to study the relaxation behavior of materials and understand their properties, such as viscosity and elasticity.
- Biophysics: The Debye relaxation process is used to study the dynamics of biological systems, such as protein folding and DNA unwinding.
Criticisms and Limitations of the Debye Relaxation Process

While the Debye relaxation process is a fundamental concept in physics and chemistry, it has several limitations and criticisms, including:
- Simplifying Assumptions: The Debye model assumes a single relaxation time and non-interacting dipoles, which are not always realistic assumptions.
- Non-Exponential Decay: Many materials exhibit non-exponential decay behavior, which is not accounted for in the Debye model.
🚨 Note: The Debye relaxation process is a classical model that does not take into account quantum effects or interactions between dipoles. Therefore, it is not suitable for studying materials with complex relaxation behavior.
Modern Developments and Extensions

In recent years, there have been several modern developments and extensions of the Debye relaxation process, including:
- Fractional Calculus: Fractional calculus has been used to extend the Debye model to describe non-exponential decay behavior.
- Distributed Relaxation Times: The concept of distributed relaxation times has been introduced to account for the complexity of relaxation behavior in materials.
Conclusion

In conclusion, the Debye relaxation process is a fundamental concept in physics and chemistry that describes the relaxation behavior of dielectric materials. While it has several limitations and criticisms, it remains a widely used model in various fields. Modern developments and extensions have improved our understanding of relaxation behavior and have enabled the study of complex materials.
What is the Debye relaxation process?
+
The Debye relaxation process is a mathematical model developed by Peter Debye in 1913 to describe the relaxation behavior of dielectric materials.
What are the key characteristics of the Debye relaxation process?
+
The Debye relaxation process is characterized by exponential decay, a single relaxation time, and temperature dependence.
What are the applications of the Debye relaxation process?
+
The Debye relaxation process has numerous applications in various fields, including dielectric spectroscopy, materials science, and biophysics.



