Disk Moment of Inertia Explained in Simple Terms

Understanding Disk Moment of Inertia
The moment of inertia is a fundamental concept in physics and engineering, and it’s essential to understand it, especially when dealing with rotating objects. In this article, we’ll delve into the world of disk moment of inertia, explaining it in simple terms, and providing examples to help you grasp this concept.
What is Moment of Inertia?

The moment of inertia is a measure of an object’s resistance to changes in its rotation. It depends on the object’s mass distribution and its shape. The more mass an object has, and the farther away that mass is from the axis of rotation, the higher its moment of inertia.
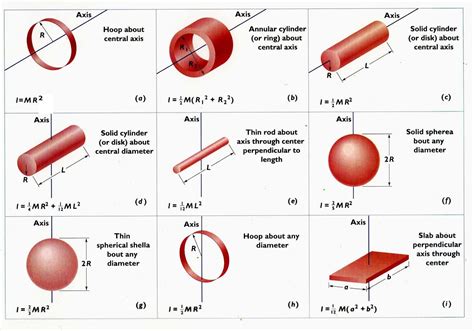
Disk Moment of Inertia

A disk is a flat, circular object, and its moment of inertia is calculated using the following formula:
I = (1⁄2) * m * r^2
where:
- I is the moment of inertia
- m is the mass of the disk
- r is the radius of the disk
This formula shows that the moment of inertia of a disk is directly proportional to its mass and the square of its radius.
How to Calculate Disk Moment of Inertia

To calculate the moment of inertia of a disk, you need to know its mass and radius. Here’s a step-by-step guide:
- Determine the mass of the disk: Measure the mass of the disk using a scale or a balance.
- Measure the radius of the disk: Measure the radius of the disk using a ruler or a caliper.
- Plug in the values: Insert the values of mass and radius into the formula: I = (1⁄2) * m * r^2
📝 Note: Make sure to use the correct units for mass (kilograms or grams) and radius (meters or centimeters).
Examples and Applications
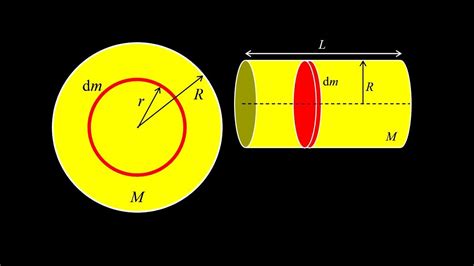
Let’s consider a few examples to illustrate the concept of disk moment of inertia:
- Example 1: A car wheel has a mass of 10 kg and a radius of 0.3 meters. Calculate its moment of inertia.
I = (1⁄2) * 10 kg * (0.3 m)^2 = 0.45 kg*m^2
- Example 2: A bicycle wheel has a mass of 2 kg and a radius of 0.25 meters. Calculate its moment of inertia.
I = (1⁄2) * 2 kg * (0.25 m)^2 = 0.0625 kg*m^2
The moment of inertia is crucial in designing and optimizing rotating systems, such as gears, wheels, and flywheels. Understanding the disk moment of inertia helps engineers to:
- Predict rotational behavior: By calculating the moment of inertia, engineers can predict how an object will rotate and respond to external forces.
- Optimize design: By minimizing the moment of inertia, engineers can reduce the energy required to rotate an object, making it more efficient.
Comparison with Other Shapes

The disk moment of inertia is different from other shapes, such as:
- Ring: The moment of inertia of a ring is I = m * r^2, which is twice that of a disk.
- Sphere: The moment of inertia of a sphere is I = (2⁄5) * m * r^2, which is less than that of a disk.
📊 Note: The moment of inertia of different shapes can be compared using the formulae and calculating the values for each shape.
Conclusion
In conclusion, the disk moment of inertia is a fundamental concept in physics and engineering, and it’s essential to understand it when dealing with rotating objects. By calculating the moment of inertia, engineers can predict rotational behavior, optimize design, and improve efficiency. Remember to use the correct units and formulae when calculating the moment of inertia, and compare it with other shapes to gain a deeper understanding of the concept.
What is the unit of moment of inertia?

+
The unit of moment of inertia is kg*m^2 or g*cm^2.
Why is the moment of inertia important in engineering?

+
The moment of inertia is crucial in designing and optimizing rotating systems, as it helps engineers to predict rotational behavior and optimize design.
How does the moment of inertia change with radius?

+
The moment of inertia increases with the square of the radius.