Karnaugh Map Solver: Simplify Digital Logic Design

Introduction to Karnaugh Maps

In the realm of digital logic design, simplifying complex circuits is crucial for optimizing performance, reducing power consumption, and minimizing hardware costs. One powerful tool for achieving this simplification is the Karnaugh map (K-map). Developed by Maurice Karnaugh in 1953, the K-map is a graphical method for minimizing Boolean algebraic expressions, which represent the core of digital logic circuits. This post will delve into the world of Karnaugh maps, exploring their application, benefits, and a step-by-step guide on how to use them to simplify digital logic design.
What are Karnaugh Maps?

A Karnaugh map is a two-dimensional representation of a truth table, which is a table that describes all possible input combinations of a digital circuit and their corresponding outputs. Essentially, a K-map helps in visualizing the relationship between inputs and outputs, making it easier to identify patterns and simplify the circuit.
Benefits of Using Karnaugh Maps

- Simplifies Complex Circuits: By minimizing Boolean expressions, K-maps help in reducing the number of logic gates required in a circuit, leading to less complex designs.
- Reduces Errors: Visualizing the truth table through a K-map reduces the likelihood of errors in the design process.
- Improves Performance: Simplified circuits result in faster operation and lower power consumption.
- Enhances Readability: K-maps provide a clear and concise way to represent digital logic, making it easier for designers to understand and analyze circuits.
How to Construct a Karnaugh Map

Constructing a K-map involves several steps:
- Identify the Number of Variables: Determine the number of input variables in your digital circuit.
- Create the Grid: Draw a grid with 2^n rows and 2^n columns, where n is the number of input variables.
- Label the Grid: Label each row and column with the possible values of the input variables.
- Fill in the Output Values: Fill in the output values for each combination of input variables, using the truth table as reference.
- Look for Adjacent Squares: Identify adjacent squares (horizontally or vertically) with the same output value.
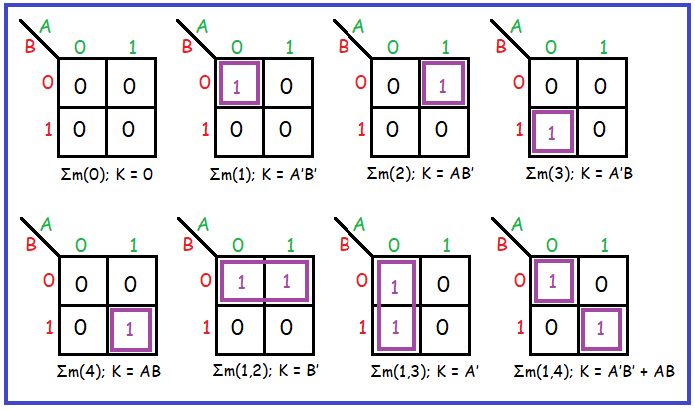
Step-by-Step Example: Simplifying a 2-Variable Circuit
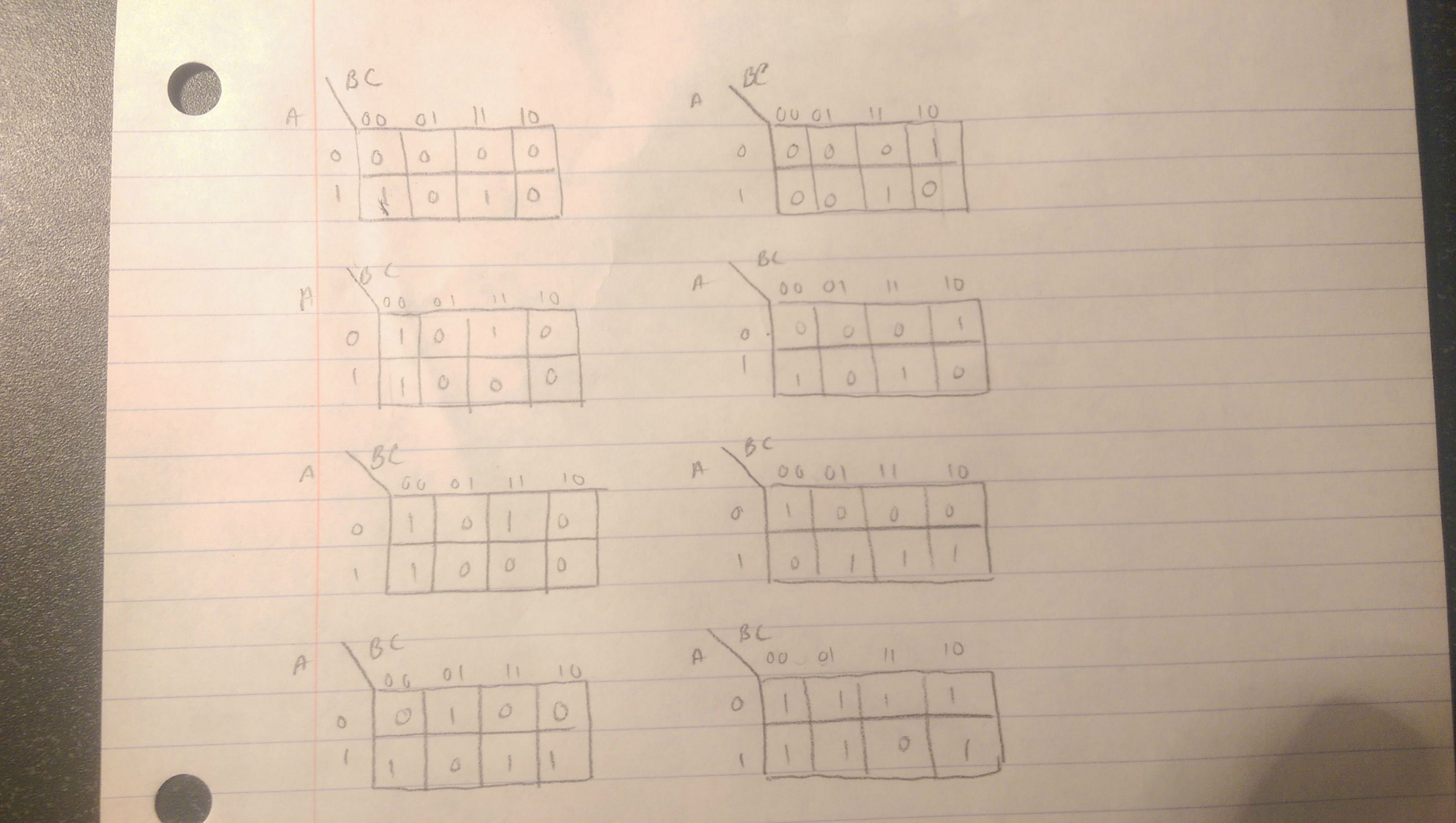
Suppose we have a digital circuit with two input variables, A and B, and an output variable, Y. The truth table for this circuit is:
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Step 1: Create the Grid
B | 0 | 1
----|----
A|0 | 0 | 1
----|----
1 | 1 | 1
Step 2: Fill in the Output Values
| B | 0 | 1 |
|---|---|---|
| A | 0 | 0 |
| —- | —- | —- |
| 1 | 1 | 1 |
Step 3: Look for Adjacent Squares
We notice that the top-right and bottom-left squares have the same output value, 1. We can group these squares together.
Simplifying the Circuit

By grouping the adjacent squares, we can simplify the circuit to:
Y = A + B
This simplified expression represents the original truth table, but with fewer logic gates.
📝 Note: In this example, we used a 2-variable K-map. For more complex circuits, you can use 3-variable or 4-variable K-maps, following a similar process.
Common Applications of Karnaugh Maps
- Digital Circuit Design: K-maps are widely used in the design of digital circuits, including combinational and sequential circuits.
- Computer Networks: K-maps can be used to optimize routing tables and improve network performance.
- Cryptography: K-maps can be applied to simplify cryptographic algorithms and improve their efficiency.
Conclusion

In conclusion, Karnaugh maps are a powerful tool for simplifying digital logic design. By following the steps outlined in this post, you can use K-maps to optimize your digital circuits, reducing complexity and improving performance. Whether you’re a student or a professional in the field of digital electronics, mastering K-maps will help you to design more efficient and effective digital systems.
What is the main advantage of using Karnaugh maps?

+
The main advantage of using Karnaugh maps is that they simplify complex digital circuits, reducing the number of logic gates required and improving performance.
Can Karnaugh maps be used for circuits with more than 4 variables?

+
Yes, Karnaugh maps can be used for circuits with more than 4 variables, but they become increasingly complex and are often replaced by other minimization techniques.
Are Karnaugh maps still relevant in modern digital design?

+
Yes, Karnaugh maps are still relevant in modern digital design, particularly in the education of digital electronics and in the design of small-scale digital systems.