5 Key Insights into Landau Fermi Liquids

Understanding the Behavior of Electrons in Metals
In the realm of condensed matter physics, the concept of Landau Fermi liquids plays a crucial role in understanding the behavior of electrons in metals. This theoretical framework, developed by Lev Landau in the 1950s, provides a robust description of the collective behavior of fermions in interacting systems. In this blog post, we will delve into the key insights of Landau Fermi liquids, exploring their significance, underlying assumptions, and implications for our understanding of electronic systems.
What is a Landau Fermi Liquid?
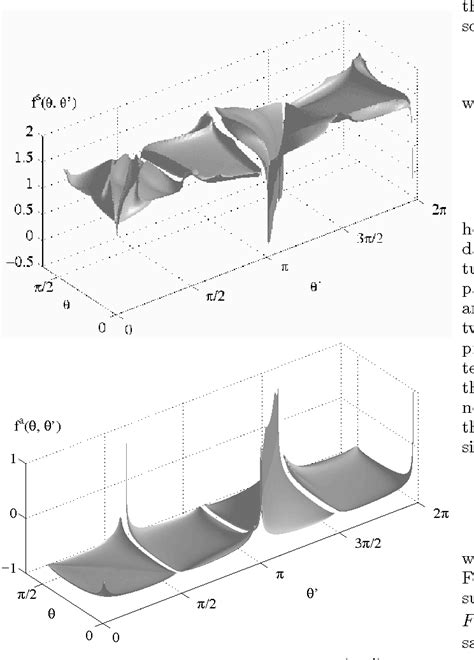
A Landau Fermi liquid is a theoretical model that describes the behavior of electrons in a metal as a collection of quasiparticles, which are composite objects comprising an electron and its surrounding cloud of electron-hole pairs. These quasiparticles behave as if they were non-interacting fermions, but with modified properties, such as effective mass and scattering rates. The Landau Fermi liquid theory assumes that the interactions between electrons can be treated as a perturbation, allowing for a one-to-one correspondence between the quasiparticles and the original electrons.
Key Assumptions and Implications
- Adiabatic Continuity: The Landau Fermi liquid theory assumes that the adiabatic continuity principle holds, meaning that the system can be transformed from a non-interacting to an interacting state without undergoing a phase transition. This assumption allows for the identification of quasiparticles and the mapping of their properties onto the original electrons.
- One-to-One Correspondence: The theory assumes that there is a one-to-one correspondence between the quasiparticles and the original electrons, ensuring that the quasiparticles retain the same spin and charge as the electrons.
- Effective Mass: The quasiparticles in a Landau Fermi liquid have an effective mass, which can differ significantly from the bare electron mass. This effective mass is a measure of the quasiparticle’s inertia and is influenced by the interactions with other electrons.
- Scattering Rates: The Landau Fermi liquid theory predicts that the quasiparticles have finite scattering rates, which determine the rate at which they interact with other quasiparticles or with impurities.
- Collective Behavior: The quasiparticles in a Landau Fermi liquid exhibit collective behavior, such as zero sound, which is a longitudinal collective mode that arises from the interactions between quasiparticles.
Experimental Evidence and Applications
The Landau Fermi liquid theory has been extensively tested and validated through numerous experiments on various metallic systems. Some of the key experimental evidence includes:
- de Haas-van Alphen Effect: The Landau Fermi liquid theory predicts that the de Haas-van Alphen effect, which is the oscillation of the magnetization with the applied magnetic field, is a direct consequence of the quasiparticle’s behavior.
- Shubnikov-de Haas Oscillations: The theory also predicts the Shubnikov-de Haas oscillations, which are the oscillations of the resistivity with the applied magnetic field.
- Fermi Liquid Parameters: The Landau Fermi liquid theory predicts the existence of Fermi liquid parameters, such as the effective mass and the scattering rates, which have been experimentally measured in various systems.
The Landau Fermi liquid theory has far-reaching implications for our understanding of electronic systems, from simple metals to complex correlated materials. It provides a robust framework for understanding the behavior of electrons in interacting systems and has been instrumental in the development of modern condensed matter physics.
💡 Note: The Landau Fermi liquid theory is a low-energy effective theory, meaning it is only applicable at low temperatures and energies, where the interactions between electrons are weak.
Conclusion

In conclusion, the Landau Fermi liquid theory provides a powerful framework for understanding the behavior of electrons in metals. By assuming adiabatic continuity, one-to-one correspondence, and effective mass, the theory predicts the collective behavior of quasiparticles, which has been extensively validated through experiments. The implications of the Landau Fermi liquid theory are far-reaching, providing a foundation for understanding the behavior of electrons in interacting systems and driving the development of modern condensed matter physics.
What is the main assumption of the Landau Fermi liquid theory?

+
The main assumption of the Landau Fermi liquid theory is the adiabatic continuity principle, which states that the system can be transformed from a non-interacting to an interacting state without undergoing a phase transition.
What is the significance of the effective mass in the Landau Fermi liquid theory?
+
The effective mass is a measure of the quasiparticle’s inertia and is influenced by the interactions with other electrons. It can differ significantly from the bare electron mass.
What is the experimental evidence for the Landau Fermi liquid theory?
+
The experimental evidence includes the de Haas-van Alphen effect, Shubnikov-de Haas oscillations, and the measurement of Fermi liquid parameters.