Mach 1 to Knots Conversion Guide

Understanding the Concept of Mach Number and Knots

The world of aviation and aerospace engineering relies heavily on precise measurements of speed, and two common units of measurement are Mach number and knots. While both units are used to express speed, they are fundamentally different in their approach and application. In this article, we will delve into the concepts of Mach number and knots, and provide a comprehensive guide on how to convert between the two.
What is Mach Number?

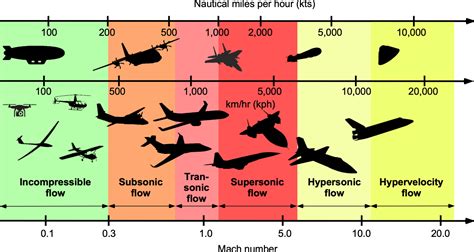
Mach number is a dimensionless quantity used to express the speed of an object relative to the speed of sound in the surrounding medium. It is named after Austrian physicist Ernst Mach, who first introduced the concept in the late 19th century. Mach number is calculated as the ratio of the object’s speed to the speed of sound in the surrounding medium, typically air.
Mach Number Formula:
Mach Number (M) = Object Speed (v) / Speed of Sound (a)
Speed of Sound:
The speed of sound in air is approximately 768 miles per hour (mph) or 1,236 kilometers per hour (km/h) at sea level in dry air at a temperature of 59 degrees Fahrenheit (15 degrees Celsius). However, the speed of sound varies with temperature, humidity, and air pressure.
What are Knots?

A knot is a unit of speed that is equal to one nautical mile per hour. A nautical mile is the length of one minute of latitude on the Earth’s surface, equivalent to 6,076.1 feet or 1,852 meters. Knots are commonly used in navigation, aviation, and meteorology to express wind speed, aircraft speed, and sailing speeds.
Mach to Knots Conversion

To convert Mach number to knots, we need to follow a two-step process:
- Calculate the speed in miles per hour (mph): Multiply the Mach number by the speed of sound in mph.
- Convert miles per hour to knots: Use the conversion factor 1 mph = 0.8689762419 knots.
Mach to Knots Conversion Formula:
Knots = (Mach Number x Speed of Sound in mph) x 0.8689762419
Example Conversion:
Suppose we want to convert a Mach number of 0.8 to knots. Assuming a speed of sound of 768 mph, we can calculate the speed in mph as follows:
Speed in mph = 0.8 x 768 mph = 614.4 mph
Now, we can convert the speed to knots:
Knots = 614.4 mph x 0.8689762419 ≈ 533.71 knots
Knots to Mach Conversion

To convert knots to Mach number, we can use the inverse of the conversion formula:
Knots to Mach Conversion Formula:
Mach Number = (Knots / 0.8689762419) / Speed of Sound in mph
Example Conversion:
Suppose we want to convert 500 knots to Mach number. Assuming a speed of sound of 768 mph, we can calculate the Mach number as follows:
Mach Number = (500 knots / 0.8689762419) / 768 mph ≈ 0.72
Conclusion

In conclusion, converting between Mach number and knots requires an understanding of the fundamental concepts of speed and the relationships between different units of measurement. By following the step-by-step guide and formulas provided in this article, you can accurately convert between Mach number and knots.
Important Considerations:
When converting between Mach number and knots, it’s essential to consider the following factors:
- Temperature and air pressure can affect the speed of sound, which in turn affects the conversion.
- The conversion formulas assume a standard atmosphere with a temperature of 59 degrees Fahrenheit (15 degrees Celsius) and an air pressure of 1 atm.
- Knots are a more intuitive unit of speed for navigation and aviation applications, while Mach number is more commonly used in aerospace engineering and supersonic flight.
What is the difference between Mach number and knots?
+
Mach number is a dimensionless quantity that expresses speed relative to the speed of sound, while knots are a unit of speed equal to one nautical mile per hour.
Why is it important to consider temperature and air pressure when converting between Mach number and knots?
+
Temperature and air pressure can affect the speed of sound, which in turn affects the conversion between Mach number and knots.
What is the standard atmosphere assumed in the conversion formulas?

+
The standard atmosphere assumed in the conversion formulas is a temperature of 59 degrees Fahrenheit (15 degrees Celsius) and an air pressure of 1 atm.



