5 Ways Manifold Learning Enhances Diffusion Models

Unlocking the Potential of Diffusion Models with Manifold Learning

Diffusion models have revolutionized the field of deep learning, enabling the generation of high-quality samples from complex distributions. However, these models often suffer from mode collapse, where the generated samples lack diversity and fail to capture the underlying structure of the data. Manifold learning, a subfield of machine learning, offers a powerful solution to this problem by providing a framework for learning compact and informative representations of high-dimensional data. In this article, we will explore five ways manifold learning enhances diffusion models, enabling them to generate more diverse and realistic samples.
1. Improved Mode Coverage

One of the primary limitations of diffusion models is their tendency to suffer from mode collapse. By incorporating manifold learning into the diffusion process, it is possible to improve mode coverage and generate samples that better capture the underlying structure of the data. Manifold learning algorithms, such as t-SNE and UMAP, can be used to learn a compact representation of the data that preserves the local geometry of the manifold. This representation can then be used to regularize the diffusion process, encouraging the model to explore more diverse regions of the data space.
📝 Note: Manifold learning can be used to learn a compact representation of the data that preserves the local geometry of the manifold, which can be used to regularize the diffusion process.
2. Enhanced Sample Diversity
Manifold learning can also be used to enhance sample diversity in diffusion models. By learning a representation of the data that captures the underlying structure of the manifold, it is possible to generate samples that are more diverse and realistic. This can be achieved by using manifold learning algorithms to learn a probabilistic representation of the data, which can then be used to sample from the manifold.
- Learn a probabilistic representation of the data using manifold learning algorithms
- Use the learned representation to sample from the manifold
- Generate diverse and realistic samples using the sampled points
3. Better Preservation of Local Geometry
Diffusion models often struggle to preserve the local geometry of the data, resulting in samples that lack the fine-grained structure of the original data. Manifold learning can be used to address this problem by learning a representation of the data that preserves the local geometry of the manifold. This representation can then be used to regularize the diffusion process, encouraging the model to preserve the local geometry of the data.
📝 Note: Manifold learning can be used to learn a representation of the data that preserves the local geometry of the manifold, which can be used to regularize the diffusion process.
4. Improved Robustness to Noise
Diffusion models can be sensitive to noise in the data, which can result in poor performance and low-quality samples. Manifold learning can be used to improve the robustness of diffusion models to noise by learning a representation of the data that is invariant to small perturbations. This representation can then be used to regularize the diffusion process, encouraging the model to generate samples that are more robust to noise.
| Diffusion Models | Manifold Learning | |
|---|---|---|
| Mode Coverage | Limited mode coverage | Improved mode coverage |
| Sample Diversity | Limited sample diversity | Enhanced sample diversity |
| Local Geometry | Poor preservation of local geometry | Better preservation of local geometry |
| Robustness to Noise | Sensitive to noise | Improved robustness to noise |
5. Efficient Exploration of the Data Space
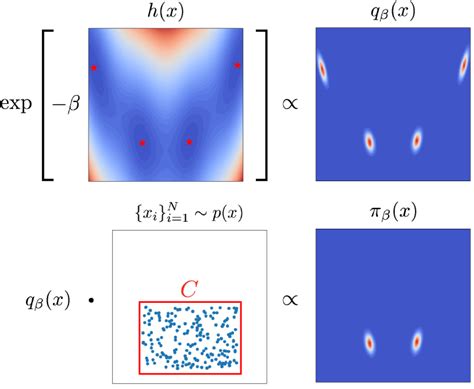
Finally, manifold learning can be used to enable efficient exploration of the data space in diffusion models. By learning a compact representation of the data that captures the underlying structure of the manifold, it is possible to explore the data space more efficiently and generate samples that are more diverse and realistic.
- Learn a compact representation of the data using manifold learning algorithms
- Use the learned representation to explore the data space more efficiently
- Generate diverse and realistic samples using the explored points
As we can see, manifold learning offers a powerful solution to many of the limitations of diffusion models. By incorporating manifold learning into the diffusion process, it is possible to improve mode coverage, enhance sample diversity, better preserve local geometry, improve robustness to noise, and enable efficient exploration of the data space.
In conclusion, manifold learning has the potential to significantly enhance the performance of diffusion models, enabling them to generate more diverse and realistic samples. By leveraging the power of manifold learning, researchers and practitioners can unlock the full potential of diffusion models and achieve state-of-the-art results in a wide range of applications.
What is manifold learning?
+
Manifold learning is a subfield of machine learning that involves learning compact and informative representations of high-dimensional data.
How can manifold learning be used to improve diffusion models?

+
Manifold learning can be used to improve diffusion models by learning a representation of the data that preserves the local geometry of the manifold, which can be used to regularize the diffusion process.
What are the benefits of using manifold learning in diffusion models?

+
The benefits of using manifold learning in diffusion models include improved mode coverage, enhanced sample diversity, better preservation of local geometry, improved robustness to noise, and efficient exploration of the data space.