Moment of Inertia of a Disk Explained Simply

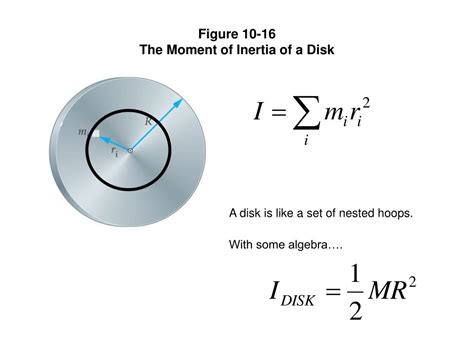
Moment of Inertia of a Disk: A Comprehensive Guide

In physics, the moment of inertia is a fundamental concept that describes the rotational inertia of an object. It plays a crucial role in understanding how objects behave when rotated around a pivot point or axis. In this article, we will delve into the concept of the moment of inertia of a disk, its definition, formula, and significance in real-world applications.

What is the Moment of Inertia of a Disk?

The moment of inertia of a disk is a measure of its resistance to changes in its rotational motion. It depends on the mass distribution of the disk and the distance of its mass elements from the axis of rotation. In simple terms, the moment of inertia of a disk determines how difficult it is to rotate or stop the disk from rotating.

Formula for the Moment of Inertia of a Disk

The moment of inertia of a disk is given by the following formula:

I = (¹⁄₂)mr^2

Where:

• I is the moment of inertia of the disk
• m is the mass of the disk
• r is the radius of the disk

This formula shows that the moment of inertia of a disk is directly proportional to its mass and the square of its radius.

Derivation of the Formula

To derive the formula for the moment of inertia of a disk, we can consider the disk as a collection of infinitesimal mass elements. Each mass element is located at a distance r from the axis of rotation and has a mass dm.

Using the definition of moment of inertia, we can write:

dI = r^2 dm

Integrating this expression over the entire disk, we get:

I = ∫r^2 dm

Since the disk is a continuous object, we can replace the integral with a summation:

I = ∑r^2 dm

Using the fact that the mass of the disk is uniform, we can rewrite the summation as:

I = (¹⁄₂)mr^2

This derivation shows that the formula for the moment of inertia of a disk is a direct result of the definition of moment of inertia and the properties of the disk.

Significance of the Moment of Inertia of a Disk

The moment of inertia of a disk has numerous applications in real-world physics and engineering. Here are a few examples:

• Rotational Kinematics: The moment of inertia of a disk is essential in understanding the rotational motion of objects. It helps us calculate the angular velocity, angular acceleration, and torque of rotating objects.
• Mechanical Engineering: The moment of inertia of a disk is crucial in designing mechanical systems, such as gearboxes, engines, and turbines. It helps engineers determine the rotational inertia of these systems and optimize their performance.
• Aerospace Engineering: The moment of inertia of a disk is essential in the design of aircraft and spacecraft. It helps engineers calculate the rotational inertia of these vehicles and ensure stable flight.

Real-World Examples

Here are a few real-world examples of the moment of inertia of a disk in action:

• Bicycle Wheels: The moment of inertia of a bicycle wheel determines how easily it can be rotated. A wheel with a higher moment of inertia requires more torque to rotate, making it more difficult to pedal.
• Car Engines: The moment of inertia of a car engine’s crankshaft affects its rotational inertia. A crankshaft with a higher moment of inertia requires more torque to rotate, which can affect the engine’s performance.
• Spacecraft: The moment of inertia of a spacecraft’s wheels or rotors determines its rotational stability. A spacecraft with a higher moment of inertia is more stable and easier to control.

📝 Note: The moment of inertia of a disk is an essential concept in physics and engineering. It helps us understand the rotational motion of objects and design mechanical systems that are efficient and stable.

🤔 Note: The formula for the moment of inertia of a disk is a simple yet powerful tool. It helps us calculate the rotational inertia of disks and predict their behavior in various situations.

In conclusion, the moment of inertia of a disk is a fundamental concept that plays a crucial role in understanding the rotational motion of objects. Its formula is a simple yet powerful tool that helps us calculate the rotational inertia of disks and predict their behavior in various situations. The significance of the moment of inertia of a disk is evident in its numerous applications in real-world physics and engineering.

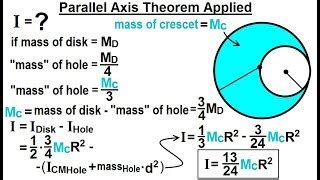
What is the moment of inertia of a disk?

+

The moment of inertia of a disk is a measure of its resistance to changes in its rotational motion. It depends on the mass distribution of the disk and the distance of its mass elements from the axis of rotation.

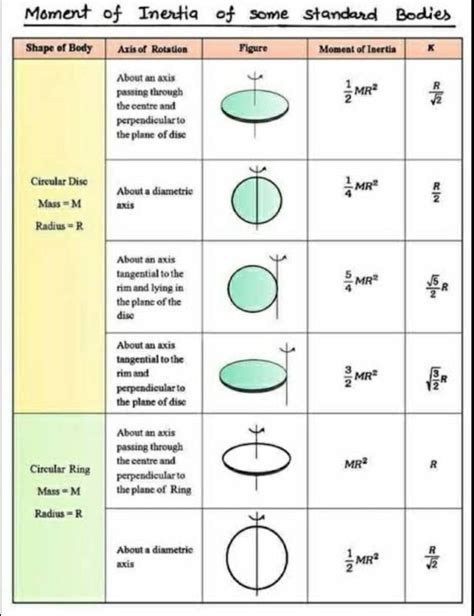
What is the formula for the moment of inertia of a disk?

+

The formula for the moment of inertia of a disk is I = (¹⁄₂)mr^2, where I is the moment of inertia, m is the mass, and r is the radius of the disk.

Why is the moment of inertia of a disk important?

+

The moment of inertia of a disk is important because it helps us understand the rotational motion of objects and design mechanical systems that are efficient and stable. It has numerous applications in real-world physics and engineering.