Monte Carlo Methods for Gaussian Processes

Introduction to Gaussian Processes and Monte Carlo Methods
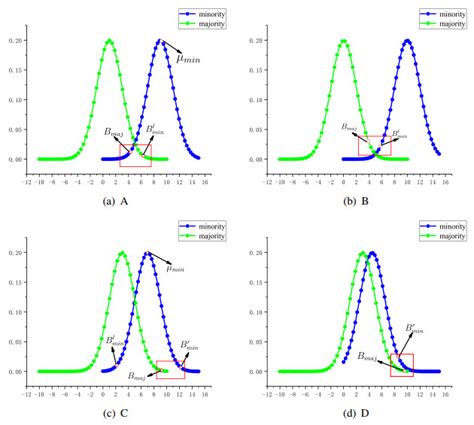
Gaussian processes (GPs) are a powerful tool for probabilistic modeling and have been widely used in machine learning, Bayesian inference, and statistical modeling. However, as the size of the dataset increases, exact inference in GPs becomes computationally expensive. This is where Monte Carlo methods come into play, providing a powerful toolkit for approximating the behavior of complex systems, including GPs.
What are Gaussian Processes?

Gaussian processes are a class of stochastic processes that are characterized by their mean and covariance functions. They are often used as a prior distribution over functions in Bayesian inference, and their flexibility and interpretability make them a popular choice in many applications.
Key Properties of Gaussian Processes:
- Mean Function: The mean function of a GP defines the expected value of the process at any given point.
- Covariance Function: The covariance function of a GP defines the correlation between the values of the process at different points.
- Marginal Distribution: The marginal distribution of a GP is multivariate normal, which makes it easy to compute the likelihood of the data.
Challenges in Gaussian Process Inference

Exact inference in GPs is often computationally expensive, especially when dealing with large datasets. The main challenges are:
- Computational Cost: Computing the covariance matrix and its inverse can be expensive, especially for large datasets.
- Scalability: As the size of the dataset increases, the number of computations required for exact inference grows exponentially.
Monte Carlo Methods for Gaussian Process Inference

Monte Carlo methods provide a way to approximate the behavior of complex systems, including GPs, by simulating random samples from the distribution. The key idea is to use these samples to estimate the quantities of interest, such as the posterior distribution or the predictive distribution.
Types of Monte Carlo Methods:
- Random Sampling: This involves sampling from the prior distribution of the GP and then weighting the samples by the likelihood of the data.
- Markov Chain Monte Carlo (MCMC): This involves constructing a Markov chain that converges to the posterior distribution of the GP.
- Importance Sampling: This involves sampling from a proposal distribution and then weighting the samples by the ratio of the posterior distribution to the proposal distribution.
Advantages of Monte Carlo Methods

Monte Carlo methods have several advantages when used for GP inference:
- Scalability: Monte Carlo methods can be used for large datasets, where exact inference is not feasible.
- Flexibility: Monte Carlo methods can be used for a wide range of GP models, including non-Gaussian likelihoods.
- Parallelization: Monte Carlo methods can be parallelized, making them suitable for distributed computing.
Challenges in Monte Carlo Methods
While Monte Carlo methods have many advantages, they also have some challenges:
- Computational Cost: Monte Carlo methods can be computationally expensive, especially for large datasets.
- Convergence: Ensuring convergence of the Markov chain or the importance sampling algorithm can be challenging.
- Variance: Monte Carlo methods can have high variance, especially if the proposal distribution is not well-chosen.
Notes on Monte Carlo Methods
📝 Note: Monte Carlo methods are not a replacement for exact inference, but rather a complementary tool for approximating the behavior of complex systems.
📝 Note: The choice of proposal distribution in importance sampling can significantly affect the performance of the algorithm.
Conclusion
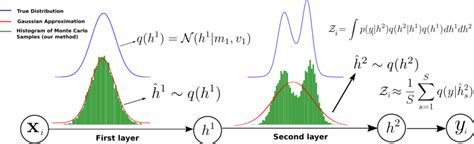
Monte Carlo methods provide a powerful toolkit for approximating the behavior of complex systems, including Gaussian processes. While they have many advantages, they also have some challenges that need to be addressed. By carefully choosing the proposal distribution, ensuring convergence, and parallelizing the computations, Monte Carlo methods can be a valuable tool for GP inference.
What is the main advantage of using Monte Carlo methods for Gaussian process inference?
+
The main advantage of using Monte Carlo methods for Gaussian process inference is scalability. Monte Carlo methods can be used for large datasets, where exact inference is not feasible.
What is the key challenge in using Monte Carlo methods for Gaussian process inference?

+
The key challenge in using Monte Carlo methods for Gaussian process inference is ensuring convergence of the Markov chain or the importance sampling algorithm.
Can Monte Carlo methods be used for non-Gaussian likelihoods?
+
Yes, Monte Carlo methods can be used for non-Gaussian likelihoods, making them a flexible tool for GP inference.



