Measuring the Universe: A Dive into the Parallax Method
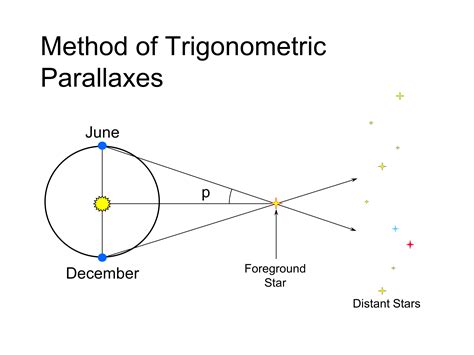
Astronomers have long been fascinated by the vast expanse of the universe, seeking to understand the distances between celestial objects. One fundamental method for measuring these distances is the parallax method, which relies on the apparent shift of nearby stars against the background of more distant stars when viewed from opposite sides of the Earth鈥檚 orbit. This method has been crucial in determining the scale of our solar system and the universe as a whole.
What is Parallax?
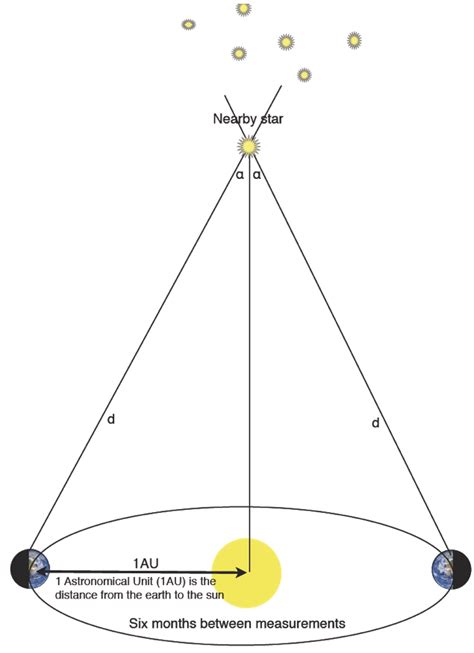
Parallax is the apparent displacement of an object against a distant background when viewed from different angles. In astronomy, this principle is applied to measure the distances to nearby stars. By observing a star from opposite sides of the Earth鈥檚 orbit, astronomers can calculate the angle of shift, known as the parallax angle. This angle is inversely proportional to the distance of the star from the Earth.
The Parallax Equation
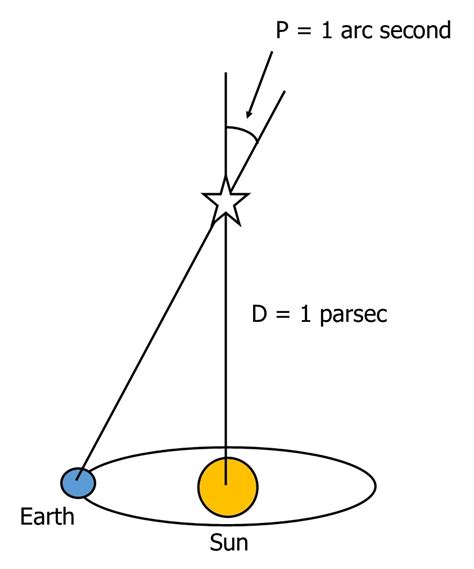
The parallax equation is a mathematical formula used to calculate the distance to a star in astronomical units (AU). The equation is based on the tangent of the parallax angle (p) and the average distance from the Earth to the Sun (1 AU = 149,597,890.7 kilometers).
Distance (in AU) = 1 / tan(p)
where p is the parallax angle in arcseconds.
How to Use the Parallax Equation
To apply the parallax equation, astronomers follow these steps:
- Measure the parallax angle (p) of a nearby star using telescopes and observational data.
- Convert the parallax angle from arcseconds to radians.
- Plug the value of p into the parallax equation to calculate the distance in AU.
馃摑 Note: The parallax equation assumes a circular orbit and neglects the effects of orbital eccentricity and other minor factors.
Challenges and Limitations
While the parallax method is a powerful tool for measuring distances, it has its limitations. The main challenge is that the parallax angle decreases with increasing distance, making it difficult to measure accurately for distant stars. Additionally, the parallax method is limited to measuring distances within a few hundred parsecs (1 parsec = 3.26 light-years).
Beyond the Parallax Method
To overcome the limitations of the parallax method, astronomers use other techniques, such as:
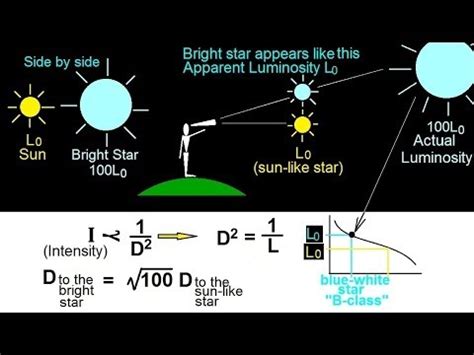
- Spectroscopic parallax: measuring the star鈥檚 spectrum to estimate its distance.
- Main-sequence fitting: using the star鈥檚 luminosity and color to estimate its distance.
- Standard candles: using supernovae or Cepheid variables as distance markers.
Conclusion
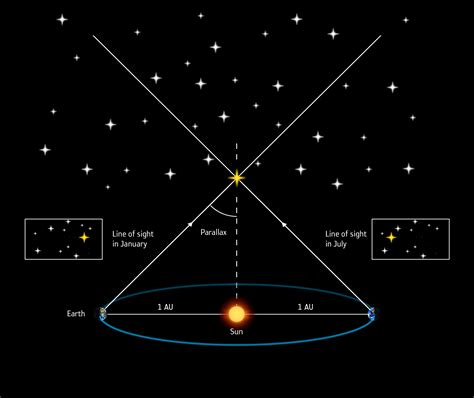
The parallax method has played a vital role in our understanding of the universe, allowing us to measure distances to nearby stars and construct a 3D map of the cosmos. While it has its limitations, the parallax equation remains a fundamental tool in astronomy, providing a foundation for more advanced distance-measuring techniques.
What is the parallax method used for?
+
The parallax method is used to measure the distances to nearby stars by observing the apparent shift of the star against the background of more distant stars when viewed from opposite sides of the Earth鈥檚 orbit.
What is the parallax equation?
+
The parallax equation is a mathematical formula used to calculate the distance to a star in astronomical units (AU): Distance (in AU) = 1 / tan(p), where p is the parallax angle in arcseconds.
What are the limitations of the parallax method?
+
The parallax method has limitations, including the difficulty in measuring the parallax angle for distant stars and the assumption of a circular orbit.
