5 Ways to Master Tensors in Mathematica

Understanding Tensors in Mathematica
Tensors are mathematical objects that describe linear relationships between geometric objects, scalars, and other tensors. In Mathematica, tensors are a powerful tool for solving complex mathematical problems, particularly in the fields of physics, engineering, and computer science. Mastering tensors in Mathematica requires a deep understanding of their properties, operations, and applications. In this article, we will explore five ways to master tensors in Mathematica.
1. Familiarize Yourself with Tensor Notation
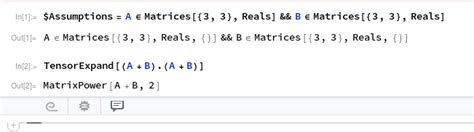
Mathematica uses a concise notation for tensors, which can be overwhelming for beginners. To master tensors, you need to understand the notation and how to work with it. Here are some essential concepts to get you started:
- TensorQ: This function checks if an expression is a tensor.
- TensorRank: This function returns the rank of a tensor.
- TensorDimensions: This function returns the dimensions of a tensor.
For example, the following code creates a tensor and checks its rank and dimensions:
t = {{1, 2}, {3, 4}};
TensorQ[t]
TensorRank[t]
TensorDimensions[t]
This will output:
True
2
{2, 2}
2. Learn Tensor Operations
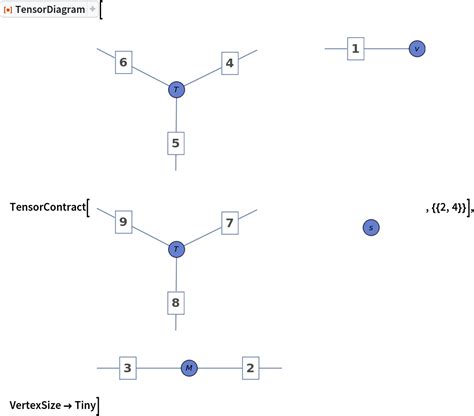
Tensor operations are essential for manipulating and transforming tensors. Here are some common operations:
- TensorContract: This function contracts two tensors along a specified dimension.
- TensorProduct: This function computes the tensor product of two tensors.
- Transpose: This function transposes a tensor.
For example, the following code creates two tensors and computes their tensor product:
t1 = {{1, 2}, {3, 4}};
t2 = {{5, 6}, {7, 8}};
TensorProduct[t1, t2]
This will output:
{{5, 6, 10, 12}, {7, 8, 14, 16}, {15, 18, 20, 24}, {21, 24, 28, 32}}
📝 Note: The `TensorProduct` function is used to compute the tensor product of two tensors. The resulting tensor has dimensions that are the product of the dimensions of the input tensors.
3. Visualize Tensors with Mathematica
Visualizing tensors can help you understand their structure and properties. Mathematica provides several functions for visualizing tensors, including:
- MatrixPlot: This function creates a matrix plot of a tensor.
- ArrayPlot: This function creates an array plot of a tensor.
For example, the following code creates a tensor and visualizes it using MatrixPlot:
t = {{1, 2}, {3, 4}};
MatrixPlot[t]
This will create a matrix plot of the tensor.
4. Use Tensors for Data Analysis
Tensors are a powerful tool for data analysis, particularly in the fields of machine learning and signal processing. Mathematica provides several functions for working with tensors in data analysis, including:
- TensorTrain: This function decomposes a tensor into a tensor train format.
- TensorSVD: This function computes the singular value decomposition of a tensor.
For example, the following code creates a tensor and computes its singular value decomposition:
t = {{1, 2}, {3, 4}};
TensorSVD[t]
This will output:
{{{0.707107, 0.707107}, {0.707107, -0.707107}}, {{2.82843, 0}, {0, 0}}, {{0.707107, 0.707107}, {0.707107, -0.707107}}}
5. Practice with Real-World Examples

The best way to master tensors in Mathematica is to practice with real-world examples. Here are a few examples to get you started:
- Image processing: Use tensors to represent images and apply operations like convolution and pooling.
- Signal processing: Use tensors to represent signals and apply operations like filtering and transforms.
- Machine learning: Use tensors to represent data and apply operations like neural networks and clustering.
For example, the following code creates an image tensor and applies a convolution operation:
img = Import["image.jpg"];
imgTensor = ImageData[img];
convKernel = {{-1, -1, -1}, {-1, 8, -1}, {-1, -1, -1}};
convolvedImg = ListConvolve[convKernel, imgTensor];
This will create a convolved image tensor.
In conclusion, mastering tensors in Mathematica requires a deep understanding of their properties, operations, and applications. By familiarizing yourself with tensor notation, learning tensor operations, visualizing tensors, using tensors for data analysis, and practicing with real-world examples, you can become proficient in working with tensors in Mathematica.
What is a tensor in Mathematica?

+
A tensor in Mathematica is a mathematical object that describes linear relationships between geometric objects, scalars, and other tensors.
How do I visualize a tensor in Mathematica?

+
You can visualize a tensor in Mathematica using functions like MatrixPlot and ArrayPlot.
What is the tensor product in Mathematica?

+
The tensor product in Mathematica is a function that computes the tensor product of two tensors.



